Eine rationale Funktion ist ein Bruchteil der Form, dessen Zähler und Nenner Polynome oder Produkte von Polynomen sind.

Beispiel 1. Schritt 2.

.

Wir multiplizieren die unbestimmten Koeffizienten mit Polynomen, die nicht in diesem einzelnen Bruch, sondern in anderen resultierenden Brüchen vorkommen:

Wir öffnen die Klammern und setzen den Zähler des ursprünglichen Integranden mit dem resultierenden Ausdruck gleich:

Auf beiden Seiten der Gleichheit suchen wir nach Termen mit gleichen Potenzen von x und stellen daraus ein Gleichungssystem auf:

.

Wir streichen alle x und erhalten ein äquivalentes Gleichungssystem:

.

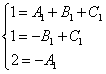Somit ist die endgültige Entwicklung des Integranden in eine Summe einfacher Brüche:

.

Beispiel 2. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Jetzt beginnen wir mit der Suche nach unsicheren Koeffizienten. Dazu setzen wir den Zähler des ursprünglichen Bruchs im Funktionsausdruck mit dem Zähler des Ausdrucks gleich, den man erhält, nachdem man die Summe der Brüche auf einen gemeinsamen Nenner reduziert hat:

Jetzt müssen Sie ein Gleichungssystem erstellen und lösen. Dazu setzen wir die Koeffizienten der Variablen mit dem entsprechenden Grad im Zähler des ursprünglichen Ausdrucks der Funktion und ähnlichen Koeffizienten im im vorherigen Schritt erhaltenen Ausdruck gleich:

Wir lösen das resultierende System:

Also, von hier aus

.

Beispiel 3. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

Wir beginnen, nach unsicheren Koeffizienten zu suchen. Dazu setzen wir den Zähler des ursprünglichen Bruchs im Funktionsausdruck mit dem Zähler des Ausdrucks gleich, den man erhält, nachdem man die Summe der Brüche auf einen gemeinsamen Nenner reduziert hat:

Wie in den vorherigen Beispielen stellen wir ein Gleichungssystem auf:

Wir reduzieren die x und erhalten ein äquivalentes Gleichungssystem:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

.

Beispiel 4. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Aus früheren Beispielen wissen wir bereits, wie man den Zähler des ursprünglichen Bruchs mit dem Ausdruck im Zähler gleichsetzt, den man erhält, nachdem man den Bruch in die Summe einfacher Brüche zerlegt und diese Summe auf einen gemeinsamen Nenner gebracht hat. Aus Gründen der Kontrolle stellen wir daher das resultierende Gleichungssystem vor:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

Beispiel 5. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Wir reduzieren diese Summe unabhängig auf einen gemeinsamen Nenner und setzen den Zähler dieses Ausdrucks mit dem Zähler des ursprünglichen Bruchs gleich. Das Ergebnis sollte das folgende Gleichungssystem sein:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

.

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

.

Beispiel 6. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

Mit diesem Betrag führen wir die gleichen Aktionen aus wie in den vorherigen Beispielen. Das Ergebnis sollte das folgende Gleichungssystem sein:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

.

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

.

Beispiel 7. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Nach bestimmten Aktionen mit der resultierenden Menge sollte sich folgendes Gleichungssystem ergeben:

Wenn wir das System lösen, erhalten wir die folgenden Werte der unsicheren Koeffizienten:

Wir erhalten die endgültige Zerlegung des Integranden in die Summe einfacher Brüche:

.

Beispiel 8. Schritt 2. In Schritt 1 haben wir die folgende Zerlegung des ursprünglichen Bruchs in die Summe einfacher Brüche mit unbestimmten Koeffizienten in den Zählern erhalten:

.

Nehmen wir einige Änderungen an den bereits automatisierten Aktionen vor, um ein Gleichungssystem zu erhalten. Es gibt eine künstliche Technik, die in manchen Fällen hilft, unnötige Berechnungen zu vermeiden. Indem wir die Summe der Brüche auf einen gemeinsamen Nenner bringen, erhalten wir und indem wir den Zähler dieses Ausdrucks mit dem Zähler des ursprünglichen Bruchs gleichsetzen, erhalten wir.

MINISTERIUM FÜR WISSENSCHAFT UND BILDUNG DER REPUBLIK BASCHKORTO STAN

SAOU SPO Baschkirische Hochschule für Architektur und Bauingenieurwesen

Khaliullin Askhat Adelzyanovich,

Mathematiklehrer in Baschkirisch

Hochschule für Architektur und Bauingenieurwesen

UFA

2014

Einleitung ___________________________________________________3

Kapitel ICH. Theoretische Aspekte der Verwendung der Methode der unsicheren Koeffizienten_____________________________________________4

Kapitel II. Sucht nach Lösungen für Probleme mit Polynomen mit der Methode der unbestimmten Koeffizienten_________________________________7

2.1.Faktorisierung eines Polynoms_____________________ 7

2.2. Probleme mit Parametern_________________________________ 10

2.3. Gleichungen lösen________________________________________14

2.4. Funktionsgleichungen______________________________19

Fazit_________________________________________________23

Liste der verwendeten Literatur________________________________________24

Anwendung ________________________________________________25

Einführung.

Diese Arbeit widmet sich den theoretischen und praktischen Aspekten der Einführung der Methode der unbestimmten Koeffizienten in den schulischen Mathematikunterricht. Die Relevanz dieses Themas wird durch die folgenden Umstände bestimmt.

Niemand wird behaupten, dass die Mathematik als Wissenschaft nicht an einem Ort steht, sie sich ständig weiterentwickelt, neue Aufgaben mit zunehmender Komplexität entstehen, was oft gewisse Schwierigkeiten mit sich bringt, da diese Aufgaben meist mit Forschung verbunden sind. In den letzten Jahren wurden solche Probleme bei Mathematikolympiaden von Schulen, Bezirken und Republiken vorgeschlagen und sind auch in den Versionen des Einheitlichen Staatsexamens verfügbar. Daher war eine spezielle Methode erforderlich, mit der zumindest einige dieser Probleme möglichst schnell, effizient und kostengünstig gelöst werden können. Diese Arbeit stellt den Inhalt der Methode der unbestimmten Koeffizienten klar dar, die in einer Vielzahl von Bereichen der Mathematik weit verbreitet ist und von Fragen des allgemeinbildenden Kurses bis hin zu seinen fortgeschrittensten Teilen reicht. Insbesondere Anwendungen der Methode der unbestimmten Koeffizienten bei der Lösung von Problemen mit Parametern, gebrochenen rationalen und funktionalen Gleichungen sind besonders interessant und effektiv; Sie können jeden, der sich für Mathematik interessiert, leicht interessieren. Der Hauptzweck der vorgeschlagenen Arbeit und Auswahl der Probleme besteht darin, umfassende Möglichkeiten zur Verbesserung und Entwicklung der Fähigkeit zu bieten, kurze und nicht standardmäßige Lösungen zu finden.

Diese Arbeit besteht aus zwei Kapiteln. Im ersten Teil werden die theoretischen Aspekte der Verwendung erörtert

Methode der unsicheren Koeffizienten und zweitens praktische und methodische Aspekte einer solchen Verwendung.

Der Anhang zur Arbeit liefert Bedingungen für konkrete Aufgaben zur eigenständigen Lösung.

Kapitel ICH . Theoretische Aspekte der Nutzung Methode der unsicheren Koeffizienten

„Der Mensch... wurde geboren, um ein Meister zu sein,

Herrscher, König der Natur, aber Weisheit,

mit der er herrschen muss, ist ihm nicht gegeben

von Geburt an: es wird durch Lernen erworben“

N. I. Lobatschewski

Es gibt verschiedene Möglichkeiten und Methoden zur Lösung von Problemen, aber eine der bequemsten, effektivsten, originellsten, elegantesten und gleichzeitig sehr einfachen und für jedermann verständlichen Methode ist die Methode der unbestimmten Koeffizienten. Die Methode der unbestimmten Koeffizienten ist eine in der Mathematik verwendete Methode, um die Koeffizienten von Ausdrücken zu ermitteln, deren Form im Voraus bekannt ist.

Bevor wir die Anwendung der Methode der unbestimmten Koeffizienten zur Lösung verschiedener Arten von Problemen betrachten, präsentieren wir eine Reihe theoretischer Informationen.

Lass sie gegeben werden

A N (X) = A 0 X N + A 1 X n-1 + A 2 X n-2 + ··· + A n-1 X + A N

B M (X ) = B 0 X M + B 1 X M -1 + B 2 X M -2 + ··· + B m-1 X + B M ,

Polynome relativ X mit irgendwelchen Chancen.

Satz. Zwei Polynome abhängig von eins und Das gleiche Argument ist genau dann identisch gleich, wennN = M und ihre entsprechenden Koeffizienten sind gleichA 0 = B 0 , A 1 = B 1 , A 2 = B 2 ,··· , A N -1 = B M -1 , A N = B M Und T. D.

Offensichtlich gelten für alle Werte gleiche Polynome X gleiche Werte. Umgekehrt, wenn die Werte zweier Polynome für alle Werte gleich sind X, dann die Polynome sind gleich, das heißt, ihre Koeffizienten haben den gleichen GradX zusammenpassen.

Daher ist die Idee, die Methode der unbestimmten Koeffizienten zur Lösung von Problemen anzuwenden, wie folgt.

Lassen Sie uns wissen, dass als Ergebnis einiger Transformationen ein Ausdruck eines bestimmten Typs erhalten wird und nur die Koeffizienten in diesem Ausdruck unbekannt sind. Dann werden diese Koeffizienten mit Buchstaben bezeichnet und als Unbekannte betrachtet. Anschließend wird ein Gleichungssystem erstellt, um diese Unbekannten zu bestimmen.

Im Fall von Polynomen werden diese Gleichungen beispielsweise unter der Bedingung erstellt, dass die Koeffizienten für die gleichen Potenzen gleich sind X für zwei gleiche Polynome.

Lassen Sie uns das oben Gesagte anhand der folgenden konkreten Beispiele demonstrieren und mit dem einfachsten beginnen.

So ergibt sich beispielsweise aufgrund theoretischer Überlegungen der Bruch

kann als Summe dargestellt werden

, Wo A , B Und C - zu bestimmende Koeffizienten. Um sie zu finden, setzen wir den zweiten Ausdruck mit dem ersten gleich:

=

und uns vom Nenner zu befreien und Begriffe mit den gleichen Befugnissen auf der linken Seite zu sammeln X, wir bekommen:

(A + B + C )X 2 + ( B - C )x - a = 2X 2 – 5 X– 1

Da die letzte Gleichheit für alle Werte gelten muss X, dann sind die Koeffizienten gleich großX rechts und links sollten gleich sein. Somit werden drei Gleichungen zur Bestimmung der drei unbekannten Koeffizienten erhalten:

a+b+c = 2

B - C = - 5

A= 1, daher A = 1 , B = - 2 , C = 3

Somit,

=
,

Die Gültigkeit dieser Gleichheit lässt sich leicht direkt überprüfen.

Angenommen, Sie müssen auch einen Bruch darstellen

als A + B
+ C
+ D
, Wo A , B , C Und D- unbekannte rationale Koeffizienten. Wir setzen den zweiten Ausdruck mit dem ersten gleich:

A + B
+ C
+ D
=
oder, Wenn wir uns vom Nenner befreien, wenn möglich rationale Faktoren unter den Zeichen der Wurzeln entfernen und ähnliche Begriffe auf die linke Seite bringen, erhalten wir:

(A- 2 B + 3 C ) + (- a+b +3 D )
+ (a+c - 2 D )
+

+ (b - c + D )
= 1 +
-
.

Eine solche Gleichheit ist jedoch nur dann möglich, wenn die rationalen Terme beider Teile und die Koeffizienten derselben Radikale gleich sind. Somit werden vier Gleichungen zum Finden der unbekannten Koeffizienten erhalten A , B , C Und D :

A- 2b+ 3C = 1

- a+b +3 D = 1

a+c - 2 D = - 1

B - C + D= 0, daher A = 0 ; B = - ; C = 0 ; D= , das heißt
= -
+
.

Kapitel II. Sucht nach Lösungen für Probleme mit Polynomen Methode der unbestimmten Koeffizienten.

„Nichts trägt besser zur Beherrschung eines Fachs bei als

die Art und Weise, in verschiedenen Situationen mit ihm umzugehen“

Akademiker B.V. Gnedenko

2. 1. Faktorisieren eines Polynoms.

Methoden zur Faktorisierung von Polynomen:

1) Setzen des gemeinsamen Faktors aus Klammern; 2) Gruppierungsmethode; 3) Anwendung grundlegender Multiplikationsformeln; 4) Einführung von Hilfstermen; 5) vorläufige Transformation eines gegebenen Polynoms unter Verwendung bestimmter Formeln; 6) Erweiterung durch Finden der Wurzeln eines gegebenen Polynoms; 7) Methode zur Eingabe des Parameters; 8)Methode der unbestimmten Koeffizienten.

Aufgabe 1. Zerlegen Sie das Polynom in reelle Faktoren X 4 + X 2 + 1 .

Lösung. Es gibt keine Wurzeln zwischen den Teilern des freien Termes dieses Polynoms. Wir können die Wurzeln des Polynoms nicht mit anderen elementaren Mitteln finden. Daher ist es nicht möglich, die erforderliche Entwicklung durchzuführen, indem zunächst die Wurzeln dieses Polynoms ermittelt werden. Es bleibt nach einer Lösung des Problems zu suchen, entweder durch Einführung von Hilfstermen oder durch die Methode der unbestimmten Koeffizienten. Es ist klar, dass X 4 + X 2 + 1 = X 4 + X 3 + X 2 - X 3 - X 2 - X + X 2 + X + 1 =

= X 2 (X 2 + X + 1) - X (X 2 + X + 1) + X 2 + X + 1 =

= (X 2 + X + 1)(X 2 - X + 1).

Die resultierenden quadratischen Trinome haben keine Wurzeln und sind daher nicht in reelle lineare Faktoren zerlegbar.

Die beschriebene Methode ist technisch einfach, aber aufgrund ihrer Künstlichkeit schwierig. Tatsächlich ist es sehr schwierig, die erforderlichen Hilfsbegriffe zu finden. Nur eine Vermutung half uns, diese Zerlegung zu finden. Aber

Es gibt zuverlässigere Möglichkeiten, solche Probleme zu lösen.

Man könnte so vorgehen: Angenommen, das gegebene Polynom zerfällt in das Produkt

(X 2 + A X + B )(X 2 + C X + D )

zwei quadratische Trinome mit ganzzahligen Koeffizienten.

Das werden wir also haben

X 4 + X 2 + 1 = (X 2 + A X + B )(X 2 + C X + D )

Es bleibt die Bestimmung der KoeffizientenA , B , C Und D .

Wenn wir die Polynome auf der rechten Seite der letzten Gleichung multiplizieren, erhalten wir:X 4 + X 2 + 1 = X 4 +

+ (a + c ) X 3 + (B + A C + D ) X 2 + (Anzeige + v. Chr ) x + bd .

Da wir aber brauchen, dass sich die rechte Seite dieser Gleichung in dasselbe Polynom wie auf der linken Seite verwandelt, müssen die folgenden Bedingungen erfüllt sein:

a + c = 0

B + A C + D = 1

Anzeige + v. Chr = 0

bd = 1 .

Das Ergebnis ist ein System aus vier Gleichungen mit vier UnbekanntenA , B , C Und D . Es ist einfach, die Koeffizienten aus diesem System zu ermittelnA = 1 , B = 1 , C = -1 Und D = 1.

Jetzt ist das Problem vollständig gelöst. Wir bekamen:

X 4 + X 2 + 1 = (X 2 + X + 1)(X 2 - X + 1).

Aufgabe 2. Faktorisieren Sie das Polynom in reelle Faktoren X 3 – 6 X 2 + 14 X – 15 .

Lösung. Stellen wir dieses Polynom in der Form dar

X 3 – 6 X 2 + 14 X – 15 = (X + A )(X 2 + bx + C) , Wo A , B Und Mit - Koeffizienten noch nicht bestimmt. Denn zwei Polynome sind genau dann identisch gleich, wenn die Koeffizienten die gleichen Potenzen habenX sind dann gleich, wobei die Koeffizienten jeweils gleichgesetzt werdenX 2 , X und freien Termen erhalten wir ein System aus drei Gleichungen mit drei Unbekannten:

a+b= - 6

ab + c = 14

ac = - 15 .

Die Lösung dieses Systems wird erheblich vereinfacht, wenn wir berücksichtigen, dass die Zahl 3 (Teiler des freien Termes) die Wurzel dieser Gleichung ist und daherA = - 3 ,

B = - 3 Und Mit = 5 .

Dann X 3 – 6 X 2 + 14 X – 15 = (X – 3)(X 2 – 3 X + 5).

Die angewandte Methode der unbestimmten Koeffizienten enthält im Vergleich zur obigen Methode der Einführung von Hilfstermen nichts Künstliches, erfordert jedoch die Anwendung vieler theoretischer Prinzipien und geht mit ziemlich umfangreichen Berechnungen einher. Für Polynome höheren Grades führt diese Methode der unbestimmten Koeffizienten zu umständlichen Gleichungssystemen.

2.2.Aufgaben und mit Parametern.

In den letzten Jahren wurden in Versionen des Einheitlichen Staatsexamens Aufgaben mit Parametern angeboten. Ihre Lösung bereitet oft gewisse Schwierigkeiten. Bei der Lösung von Problemen mit Parametern können Sie neben anderen Methoden auch die Methode der unbestimmten Koeffizienten sehr effektiv verwenden. Mit dieser Methode können Sie die Lösung erheblich vereinfachen und schnell eine Antwort erhalten.

Aufgabe 3. Bestimmen Sie, bei welchen Werten der Parameter vorliegt A Gleichung 2 X 3 – 3 X 2 – 36 X + A – 3 = 0 hat genau zwei Wurzeln.

Lösung. 1 Weg. Ableitung verwenden.

Stellen wir diese Gleichung in Form von zwei Funktionen dar

2x 3 – 3 X 2 – 36 X – 3 = – A .

F (X) = 2x 3 – 3 X 2 – 36 X– 3 und φ( X ) = – A .

Lassen Sie uns die Funktion untersuchenF (X) = 2x 3 – 3 X 2 – 36 X – 3 Verwenden Sie die Ableitung und konstruieren Sie schematisch ihren Graphen (Abb. 1.).

F( – X )F (X ) , F (– X ) – F (X ). Die Funktion ist weder gerade noch ungerade.

3. Finden wir die kritischen Punkte der Funktion, ihre Anstiegs- und Abfallintervalle, Extrema. F / (X ) = 6 X 2 – 6 X – 36. D (F / ) = R , daher werden wir alle kritischen Punkte der Funktion finden, indem wir die Gleichung lösen F / (X ) = 0 .

6(X 2 – X– 6) = 0 ,

X 2 – X– 6 = 0 ,

X 1 = 3 , X 2 = – 2 durch den Satz, der zum Satz von Vieta invers ist.

F / (X ) = 6(X – 3)(X + 2).

+ max - Mindest +

2 3 X

F / (X) > 0 für alle X< - 2 und X > 3 und die Funktion ist punktweise stetigx =- 2 und X = 3, daher nimmt es in jedem der Intervalle zu (- ; - 2] und [ 3 ; ).

F / (X ) < 0 bei - 2 < X< 3, daher nimmt es im Intervall [- 2; 3 ].

X = - 2. maximaler Punkt, weil An diesem Punkt ändert sich das Vorzeichen der Ableitung„+“ bis „-“.

F (– 2) = 2· (– 8) – 3·4 – 36·(– 2) – 3 = – 16 – 12 + 72 – 3 == 72 – 31 = 41 ,

x = 3 Mindestpunkt, da sich an dieser Stelle das Vorzeichen der Ableitung ändert„-“ bis „+“.

F (3) = 2·27 – 3·9 – 36·3 – 3 = 54 – 27 – 108 – 3 = – 138 + +54 = – 84.

Graph der Funktion φ(X ) = – A ist eine gerade Linie parallel zur x-Achse und durch den Punkt mit den Koordinaten (0; – A ). Die Diagramme haben zwei gemeinsame Punkte:A= 41, d.h. a =– 41 und – A= – 84, d.h. A = 84 .

bei

41φ( X)

2 3 X

3 F ( X ) = 2x 3 – 3 X 2 – 36 X – 3

Methode 2. Methode unbestimmter Koeffizienten.

Da diese Gleichung nach den Bedingungen des Problems nur zwei Wurzeln haben darf, liegt die Gleichheit auf der Hand:

2X 3 – 3 X 2 – 36 X + A – 3 = (x + B ) 2 (2 X + C ) ,

2X 3 – 3 X 2 – 36 X + A – 3 = 2 X 3 + (4 B + C ) X 2 + (2 B 2 + +2 v. Chr ) X + B 2 C ,

Nun werden die Koeffizienten mit den gleichen Graden gleichgesetzt X, erhalten wir ein Gleichungssystem

4 b + c = - 3

2B 2 + 2bc = - 36

B 2 C = A – 3 .

Aus den ersten beiden Gleichungen des Systems finden wirB 2 + B – 6 = 0, daher B 1 = - 3 oder B 2 = 2 . Entsprechende WerteMit 1 und Mit 2 leicht aus der ersten Gleichung des Systems zu finden:Mit 1 = 9 oder Mit 2 = - 11 . Abschließend lässt sich der gewünschte Wert des Parameters aus der letzten Gleichung des Systems ermitteln:

A = B 2 C + 3 , A 1 = - 41 oder A 2 = 84.

Antwort: Diese Gleichung hat genau zwei verschiedene

root bei A= - 41 und A= 84 .

Aufgabe 4. Finden Sie den größten Wert des ParametersA , für die die GleichungX 3 + 5 X 2 + Oh + B = 0

mit ganzzahligen Koeffizienten hat drei verschiedene Wurzeln, von denen eine gleich – 2 ist.

Lösung. 1 Weg. Ersetzen X= - 2 auf der linken Seite der Gleichung erhalten wir

8 + 20 – 2 A + B= 0, was bedeutet B = 2 A – 12 .

Da die Zahl - 2 eine Wurzel ist, können wir den gemeinsamen Faktor herausnehmen X + 2:

X 3 + 5 X 2 + Oh + B = X 3 + 2 X 2 + 3 X 2 + Oh + (2 A – 12) =

= X 2 (X + 2) + 3 X (X + 2) – 6 X + Oh + (2 A – 12) =

= X 2 (X + 2) + 3 X (X + 2) + (A – 6)(X +2) - 2(A – 6)+ (2 A - 12) =

= (X + 2)(X 2 + 3 X + (A – 6) ) .

Bedingt durch die Bedingung gibt es zwei weitere Wurzeln der Gleichung. Dies bedeutet, dass die Diskriminante des zweiten Faktors positiv ist.

D =3 2 - 4 (A – 6) = 33 – 4 A > 0, das heißt A < 8,25 .

Es scheint, dass die Antwort lauten würde a = 8 . Aber wenn wir die Zahl 8 in die ursprüngliche Gleichung einsetzen, erhalten wir:

X 3 + 5 X 2 + Oh + B = X 3 + 5 X 2 + 8 X + 4 = (X + 2)(X 2 + 3 X + 2 ) =

= (X + 1) (X + 2) 2 ,

das heißt, die Gleichung hat nur zwei verschiedene Wurzeln. Aber wenn a = 7 erzeugt tatsächlich drei verschiedene Wurzeln.

Methode 2. Methode unbestimmter Koeffizienten.

Wenn die Gleichung X 3 + 5 X 2 + Oh + B = 0 hat eine Wurzel X = - 2, dann können Sie die Zahlen jederzeit abrufenC Und D damit vor allenX Gleichheit war wahr

X 3 + 5 X 2 + Oh + B = (X + 2)(X 2 + Mit X + D ).

Zahlen findenC Und D Öffnen wir die Klammern auf der rechten Seite, fügen ähnliche Begriffe hinzu und erhalten

X 3 + 5 X 2 + Oh + B = X 3 + (2 + Mit ) X 2 +(2 s + D ) X + 2 D

Gleichsetzen der Koeffizienten bei den entsprechenden Potenzen X Wir haben ein System

2 + Mit = 5

2 Mit + D = A

2 D = B , Wo c = 3 .

Somit, X 2 + 3 X + D = 0 , D = 9 – 4 D > 0 oder

D < 2,25, also D (- ; 2 ].

Die Problembedingungen werden durch den Wert erfüllt D = 1 . Der endgültige gewünschte Wert des ParametersA = 7.

ANTWORT: Wann a = 7 Diese Gleichung hat drei verschiedene Wurzeln.

2.3. Gleichungen lösen.

„Denken Sie daran, indem Sie kleine Probleme lösen

Bereiten Sie sich darauf vor, Großes und Schwieriges in Angriff zu nehmen

neue Aufgaben.“

Akademiker S.L. Sobolev

Beim Lösen einiger Gleichungen können und sollten Sie Einfallsreichtum und Witz zeigen und spezielle Techniken anwenden. Die Beherrschung verschiedener Transformationstechniken und die Fähigkeit zum logischen Denken sind in der Mathematik von großer Bedeutung. Einer dieser Tricks besteht darin, einen ausgewählten Ausdruck oder eine bestimmte Zahl zu addieren und zu subtrahieren. Die dargelegte Tatsache selbst ist natürlich jedem bekannt – die Hauptschwierigkeit besteht darin, in einer bestimmten Konfiguration diejenigen Transformationen von Gleichungen zu sehen, auf die es bequem und zweckmäßig ist, sie anzuwenden.

Anhand einer einfachen algebraischen Gleichung veranschaulichen wir eine nicht standardmäßige Technik zum Lösen von Gleichungen.

Aufgabe 5. Lösen Sie die Gleichung

=
.

Lösung. Lassen Sie uns beide Seiten dieser Gleichung mit 5 multiplizieren und sie wie folgt umschreiben

= 0 ; X 0; -
;

= 0 ,

= 0 ,

= 0 oder
= 0

Lösen wir die resultierenden Gleichungen mit der Methode der unbestimmten Koeffizienten

X 4 - X 3 –7 X – 3 = (X 2 + ah + B )(X 2 + cx + D ) = 0

X 4 - X 3 –7 X – 3 = X 4 + (a + c ) X 3 + (B + A C + D ) X 2 + (Anzeige + v. Chr ) x+ + bd

Gleichsetzung der Koeffizienten bei X 3 , X 2 , X und kostenlose Konditionen, wir bekommen das System

a + c = -1

B + A C + D = 0

Anzeige + v. Chr = -7

bd = -3, woher wir finden:A = -2 ; B = - 1 ;

Mit = 1 ; D = 3 .

Also X 4 - X 3 –7X– 3 = (X 2 – 2 X – 1)(X 2 + X + 3) = 0 ,

X 2 – 2 X– 1 = 0 oder X 2 + X + 3 = 0

X 1,2 =
Keine Wurzeln.

Ebenso haben wir

X 4 – 12X – 5 = (X 2 – 2 X – 1)(X 2 + 2X + 5) = 0 ,

Wo X 2 + 2 X + 5 = 0 , D = - 16 < 0 , нет корней.

Antwort: X 1,2 =

Aufgabe 6. Lösen Sie die Gleichung

= 10.

Lösung. Um diese Gleichung zu lösen, müssen Sie Zahlen auswählenA Und B sodass die Zähler beider Brüche gleich sind. Deshalb haben wir das System:

= 0 , X 0; -1 ; -

= - 10

Die Aufgabe besteht also darin, die Zahlen zu findenA Und B , für die Gleichheit gilt

(ein + 6) X 2 + ach – 5 = X 2 + (5 + 2 B ) X + B

Nach dem Satz über die Gleichheit der Polynome ist es nun notwendig, dass die rechte Seite dieser Gleichheit in dasselbe Polynom übergeht wie auf der linken Seite.

Mit anderen Worten: Die Beziehungen müssen erfüllt sein

ein + 6 = 1

A = 5 + 2 B

– 5 = B , von wo aus wir die Werte findenA = - 5 ;

B = - 5 .

Bei diesen WertenA Und B Gleichwertigkeit A + B = - 10 ist auch fair.

= 0 , X 0; -1 ; -

= 0 ,

= 0 ,

(X 2 – 5X– 5)(X 2 + 3X + 1) = 0 ,

X 2 – 5X– 5 = 0 oder X 2 + 3X + 1 = 0 ,

X 1,2 =
, X 3,4 =

Antwort: X 1,2 =
, X 3,4 =

Aufgabe 7. Lösen Sie die Gleichung

= 4

Lösung. Diese Gleichung ist komplexer als die vorherigen und daher werden wir sie wie folgt gruppieren: X 0;-1;3;-8;12

0 ,

= - 4.

Aus der Bedingung der Gleichheit zweier Polynome

Oh 2 + (ein + 6) X + 12 = X 2 + (B + 11) X – 3 B ,

Wir erhalten und lösen ein Gleichungssystem für unbekannte KoeffizientenA Und B :

A = 1

ein + 6 = B + 11

12 = – 3 B , Wo a = 1 , B = - 4 .

Polynome - 3 – 6X + cx 2 + 8 cx Und X 2 + 21 + 12 D – dx sind einander nur dann identisch, wenn

Mit = 1

8 Mit - 6 = - D

3 = 21 + 12 D , Mit = 1 , D = - 2 .

Mit Wertena = 1 , B = - 4 , Mit = 1 , D = - 2

Gleichwertigkeit
= - 4 ist richtig.

Infolgedessen nimmt diese Gleichung die folgende Form an:

= 0 oder
= 0 oder
= 0 ,

= - 4 , = - 3 , = 1 , = -
.

Aus den betrachteten Beispielen wird deutlich, wie der geschickte Einsatz der Methode der unbestimmten Koeffizienten,

hilft, die Lösung einer ziemlich komplexen, ungewöhnlichen Gleichung zu vereinfachen.

2.4. Funktionsgleichungen.

„Der höchste Zweck der Mathematik... ist

ist es, die verborgene Ordnung darin zu finden

Chaos, das uns umgibt“

N. Viner

Funktionsgleichungen sind eine sehr allgemeine Klasse von Gleichungen, in denen die unbekannte Funktion eine bestimmte Funktion ist. Unter einer Funktionsgleichung im engeren Sinne werden Gleichungen verstanden, bei denen die gewünschten Funktionen durch die Bildung einer komplexen Funktion mit bekannten Funktionen einer oder mehrerer Variablen in Beziehung gesetzt werden. Eine Funktionsgleichung kann auch als Ausdruck einer Eigenschaft betrachtet werden, die eine bestimmte Klasse von Funktionen charakterisiert

[zum Beispiel Funktionsgleichung F ( X ) = F (- X ) charakterisiert die Klasse der geraden Funktionen, die FunktionsgleichungF (X + 1) = F (X ) – Klasse von Funktionen mit Periode 1 usw.].

Eine der einfachsten Funktionsgleichungen ist die GleichungF (X + j ) = F (X ) + F (j ). Kontinuierliche Lösungen dieser Funktionsgleichung haben die Form

F (X ) = CX . In der Klasse der unstetigen Funktionen hat diese Funktionsgleichung jedoch andere Lösungen. Mit der betrachteten Funktionsgleichung verbunden sind

F (X + j ) = F (X ) · F (j ), F (X j ) = F (X ) + F (j ), F (X j ) = F (X )· F (j ),

kontinuierliche Lösungen, die jeweils die Form haben

e cx , MITlnX , X α (X > 0).

Somit können diese Funktionsgleichungen zur Definition von Exponential-, Logarithmus- und Potenzfunktionen verwendet werden.

Am häufigsten werden Gleichungen für komplexe Funktionen verwendet, bei denen die erforderlichen Funktionen externe Funktionen sind. Theoretische und praktische Anwendungen

Es waren genau diese Gleichungen, die herausragende Mathematiker dazu veranlassten, sie zu studieren.

Zum Beispiel, bei Ausrichtung

F 2 (X) = F (X - j)· F (X + j)

N. I. LobatschewskiWird zur Bestimmung des Parallelitätswinkels in meiner Geometrie verwendet.

In den letzten Jahren werden bei Mathematikolympiaden häufig Aufgaben zur Lösung von Funktionsgleichungen angeboten. Ihre Lösung erfordert keine Kenntnisse, die über den Rahmen des Mathematiklehrplans an weiterführenden Schulen hinausgehen. Allerdings bereitet die Lösung von Funktionsgleichungen oft gewisse Schwierigkeiten.

Eine Möglichkeit, Lösungen für Funktionsgleichungen zu finden, ist die Methode der unbestimmten Koeffizienten. Es kann verwendet werden, wenn die allgemeine Form der gewünschten Funktion durch das Aussehen der Gleichung bestimmt werden kann. Dies gilt vor allem für die Fälle, in denen Lösungen für Gleichungen unter ganzzahligen oder gebrochenen rationalen Funktionen gesucht werden sollen.

Lassen Sie uns die Essenz dieser Technik skizzieren, indem wir die folgenden Probleme lösen.

Aufgabe 8. FunktionF (X ) ist für alle reellen x definiert und erfüllt für alleX R Zustand

3 F(X) - 2 F(1- X) = X 2 .

FindenF (X ).

Lösung. Da auf der linken Seite dieser Gleichung die unabhängige Variable x und die Werte der Funktion stehenF Werden nur lineare Operationen ausgeführt und ist die rechte Seite der Gleichung eine quadratische Funktion, dann ist es natürlich anzunehmen, dass die gewünschte Funktion ebenfalls quadratisch ist:

F (X) = Axt 2 + bx + C , WoA, B, C – zu bestimmende Koeffizienten, also unsichere Koeffizienten.

Wenn wir die Funktion in die Gleichung einsetzen, erhalten wir die Identität:

3(Axt 2 + bx+ c) – 2(A(1 – X) 2 + B(1 – X) + C) = X 2 .

Axt 2 + (5 B + 4 A) X + (C – 2 A – 2 B) = X 2 .

Zwei Polynome sind identisch gleich, wenn sie gleich sind

Koeffizienten für die gleichen Potenzen der Variablen:

A = 1

5B + 4A = 0

C– 2 A – 2 B = 0.

Aus diesem System ermitteln wir die Koeffizienten

A = 1 , B = - , C = , AuchbefriedigtGleichwertigkeit

3 F (X ) - 2 F (1- X ) = X 2 auf der Menge aller reellen Zahlen. Gleichzeitig gibt es solcheX 0 Aufgabe 9. Funktiony =F(X) für alle x ist definiert, stetig und erfüllt die BedingungF (F (X)) – F(X) = 1 + 2 X . Finden Sie zwei solcher Funktionen.

Lösung. An der gewünschten Funktion werden zwei Aktionen ausgeführt – der Vorgang des Zusammenstellens einer komplexen Funktion und

Subtraktion. Wenn man bedenkt, dass die rechte Seite der Gleichung eine lineare Funktion ist, ist es naheliegend anzunehmen, dass die gewünschte Funktion ebenfalls linear ist:F(X) = ah +B , WoA UndB – unsichere Koeffizienten. Ersetzen dieser Funktion inF (F ( (X ) = - X - 1 ;

F 2 (X ) = 2 X+ , die Lösungen der Funktionsgleichung sindF (F (X)) – F(X) = 1 + 2 X .

Abschluss.

Zusammenfassend ist festzuhalten, dass diese Arbeit sicherlich zur weiteren Erforschung einer originellen und effektiven Methode zur Lösung einer Vielzahl mathematischer Probleme beitragen wird, bei denen es sich um Probleme mit erhöhtem Schwierigkeitsgrad handelt, die tiefe Kenntnisse des Schulmathematikkurses und ein hohes logisches Denken erfordern Kultur. Wer seine Mathematikkenntnisse selbstständig vertiefen möchte, findet auch in diesem Werk Stoff zum Nachdenken und interessante Aufgaben, deren Lösung Nutzen und Zufriedenheit bringt.

Die Arbeit legt im Rahmen des bestehenden Schullehrplans und in einer für eine effektive Wahrnehmung zugänglichen Form die Methode der unbestimmten Koeffizienten dar, die zur Vertiefung des Schulunterrichts in Mathematik beiträgt.

Natürlich können nicht alle Möglichkeiten der Methode der unbestimmten Koeffizienten in einer Arbeit aufgezeigt werden. Tatsächlich bedarf die Methode noch weiterer Studien und Forschung.

Liste der verwendeten Literatur.

Glazer G.I..Geschichte der Mathematik in der Schule.-M.: Bildung, 1983.

Gomonov S.A. Funktionsgleichungen im Schulmathematikkurs // Mathematik in der Schule. – 2000. –№10 .

Dorofeev G.V., Potapov M.K., Rozov N.H.. Ein Handbuch zur Mathematik. - M.: Nauka, 1972.

Kurosh A.G.. Algebraische Gleichungen beliebiger Grade. - M.: Nauka, 1983.

Likhtarnikov L.M.. Grundlegende Einführung in Funktionsgleichungen. - St. Petersburg. : Lan, 1997.

Manturov O.V., Solntsev Yu.K., Sorokin Yu.I., Fedin N.G.. Erklärendes Wörterbuch mathematischer Begriffe.-M.: Bildung, 1971

Modenov V.P.. Ein Handbuch zur Mathematik. Teil 1.-M.: Moskauer Staatliche Universität, 1977.

Modenov V.P.. Probleme mit Parametern. - M.: Prüfung, 2006.

Potapov M.K., Aleksandrov V.V., Pasichenko P.I.. Algebra und Analyse elementarer Funktionen. - M.: Nauka, 1980.

Khaliullin A.A.. Du kannst es einfacher lösen // Mathematik in der Schule. – 2003 . - №8 .

Khaliullin.

4. Erweitern Sie Polynom 2X 4 – 5X 3 + 9X 2 – 5X+ 3 für Multiplikatoren mit ganzzahligen Koeffizienten.

5. Zu welchem ​​​​Wert A X 3 + 6X 2 + Oh+ 12 pro X+ 4 ?

6. Bei welchem ​​Wert des ParametersA Die gleichungX 3 +5 X 2 + + Oh + B = 0 mit ganzzahligen Koeffizienten hat zwei verschiedene Wurzeln, von denen eine 1 ist ?

7. Unter den Wurzeln des Polynoms X 4 + X 3 – 18X 2 + Oh + B Bei ganzzahligen Koeffizienten gibt es drei gleiche ganze Zahlen. Finden Sie den Wert B .

8. Finden Sie den größten ganzzahligen Wert des Parameters A, bei dem die Gleichung X 3 – 8X 2 + ah +B = 0 mit ganzzahligen Koeffizienten hat drei verschiedene Wurzeln, von denen eine gleich 2 ist.

9. Bei welchen Werten A Und B Die Division erfolgt ohne Rest X 4 + 3X 3 – 2X 2 + Oh + B An X 2 – 3X + 2 ?

10. Faktorpolynome:

A)X 4 + 2 X 2 – X + 2 V)X 4 – 4X 3 +9X 2 –8X + 5 D)X 4 + 12X – 5

B)X 4 + 3X 2 + 2X + 3 G)X 4 – 3X –2 e)X 4 – 7X 2 + 1 .

11. Lösen Sie die Gleichungen:

A)
= 2 = 2 F (1 – X ) = X 2 .

Finden F (X) .

13. Funktion bei= F (X) Vor allen X definiert, kontinuierlich ist und die Bedingung erfüllt F ( F (X)) = F (X) + X. Finden Sie zwei solcher Funktionen.

Gleichheit (I) ist Identität. Wenn wir es auf eine ganzzahlige Form reduzieren, erhalten wir die Gleichheit zweier Polynome. Eine solche Gleichheit ist jedoch immer nur unter der Bedingung der Term-für-Term-Gleichheit dieser Polynome erfüllt.

Indem wir die Koeffizienten für die gleichen Potenzen von x auf der linken und rechten Seite der Gleichung gleichsetzen, erhalten wir ein System linearer Gleichungen für unbekannte Koeffizienten, die gelöst werden müssen.

Da die Entwicklung (I) immer für jeden echten rationalen Bruch existiert, ist das resultierende System immer konsistent.

Diese Methode zum Ermitteln von Koeffizienten wird als Methode der unsicheren Koeffizienten (eine Methode zum Vergleichen von Koeffizienten) bezeichnet.

Lassen Sie uns ein Beispiel für die Zerlegung einer rationalen Funktion in Elementarbrüche geben.

Beispiel 6.6.27. Zerlegen Sie Brüche in Elementarbrüche.

Setze die letzte Gleichung in die zweite ein

Auf diese Weise,
.

x=2 ;

x=3 .

Sollen; .

Die Teilwertmethode erfordert weniger Arbeit und verdient daher besondere Aufmerksamkeit bei der Integration rationaler Brüche.

Wenn die Wurzeln des Nenners nur reell sind, empfiehlt es sich, diese Methode zur Bestimmung unbekannter Koeffizienten zu verwenden.

In anderen Fällen können beide Methoden kombiniert werden, um unbekannte Koeffizienten zu ermitteln.

Kommentar. Auch in anderen Fällen wird die Methode der Teilwerte verwendet, allerdings muss hier die Identität differenziert werden.

Um echte rationale Brüche zu integrieren, reicht es daher aus, Folgendes zu können:

1) Elementarbrüche integrieren;

2) Zerlegen Sie rationale Brüche in elementare Brüche.

3. Integration rationaler Brüche

Schema zur Integration rationaler Brüche:

Rationale Brüche integrieren ;

Wenn P(x) und Q(x) Polynome mit reellen Koeffizienten sind, werden drei Schritte nacheinander ausgeführt.

Erster Schritt. Wenn der Bruch unecht ist, das heißt, der Grad des Zählers P(x) größer oder gleich dem Grad des Nenners Q(x) ist, isolieren Sie den ganzen Teil des rationalen Bruchs, indem Sie den Zähler durch den Nenner entsprechend dividieren zur Regel zur Division eines Polynoms durch ein Polynom. Danach kann der rationale Bruch als Summe geschrieben werden:

1) der ausgewählte ganzzahlige Teil – das Polynom M(x);

2) echter Restbruch :

Zweiter Schritt.

Richtiger Restbruch in aufeinanderfolgende Brüche zerlegt.

Finden Sie dazu die Wurzeln der Gleichung Q(x)=0 und zerlegen Sie den Nenner Q(x) in Faktoren ersten und zweiten Grades mit reellen Koeffizienten:

Bei dieser Erweiterung des Nenners entsprechen die Faktoren 1. Grades reellen Wurzeln und die Faktoren 2. Grades parallelkonjugierten Wurzeln.

Der Koeffizient für einen größeren Grad von x im Nenner Q(x) kann als gleich 1 betrachtet werden, da dies immer durch Division von P(x) und Q(x) dadurch erreicht werden kann.

Danach wird der eigentliche Restbruch in einfachste (Elementar-)Brüche zerlegt.

Dritter Schritt. Finden Sie die Integrale des ausgewählten ganzzahligen Teils und aller Elementarbrüche (mit den oben beschriebenen Methoden), die dann addiert werden.

Beispiel6.6.28.

Unter dem Integralzeichen gibt es einen unechten rationalen Bruch, da der Grad des Zählers gleich dem Grad des Nenners ist, also wählen wir den ganzzahligen Teil.